Das Vermeiden von Fehlausbrüchen mit verfrühten Ein‑ oder Ausstiegen ist eine der am häufigsten genannten Anforderungen an ein gutes Trading‑Setup . Möchte man neben der Analyse und den besprochenen Setups auch noch das Risiko von Fehltrades, Bullen‑ oder Bärenfallen reduzieren, bietet sich folgende Methode an: Risikoabsicherung gegen Fehltrades mit Reverse Extensions.

Thomas May

Anwendung der Fibonacci-Methode im Trading (Teil 3)

Risikoabsicherung gegen Fehltrades mit Reverse Extensions

Mit sogenannten Reverse Extensions ermittelt man Preiskorridore, die der Kurs zusätzlich zu markanten Hoch‑ oder Tiefpunkten überwinden muss, um ein entsprechendes Signal zur Wiederaufnahme des ursprünglichen Trends oder zum Start einer Gegenbewegung zu liefern. Idealerweise wendet man Reverse Extensions am Ende einer Trendphase beim Übergang in eine Seitwärtsphase an. Dieser Preispuffer reduziert die Gefahr vom Einstieg in einen Fehlausbruch und hilft, in der Gegenrichtung Stopps zu platzieren, deren Bruch zugleich eine Trendwende indiziert und den Stopp damit besonders valide werden lässt. Einzige Bedingung für das Eintragen von Reverse Extensions ist, dass diese Korrektur bisher nicht mehr als 38,2 Prozent des vorherigen Trends retracen konnte.

Abbildung 23: Reverse Extensions im Modell

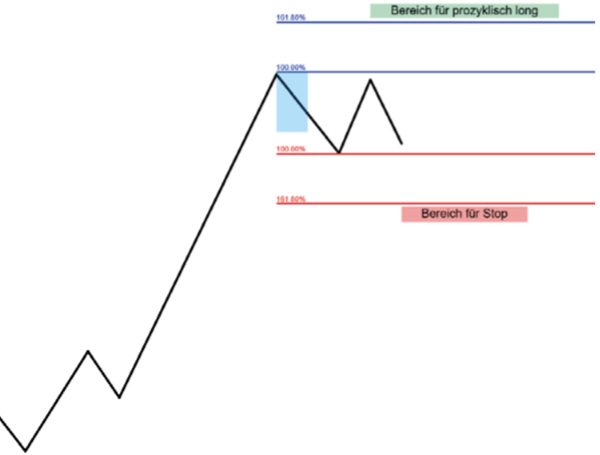
Zur Konstruktion muss lediglich die gegen den Trend gerichtete maximale Handelsspanne der laufenden Korrektur mit einem Fibonacci‑Werkzeug umfasst werden. Die Extensionen der Korrektur müssen jedoch in Trendrichtung und Gegentrendrichtung zugleich abgetragen werden. Man beschränkt sich dabei auf die 161,8‑Prozent‑Extensionen der Handelsspanne und erhält ober‑ und unterhalb der Korrektur zwei zusätzliche Kurslevels, die später zusätzlich durchschritten werden müssen, um ein Signal zu liefern. Mit diesem Korridor berechnet man im Prinzip virtuelle Preismarken, die eine Korrektur noch erreichen darf, um nicht als neue Bewegung zu gelten. Wird dieses Preislevel jedoch überwunden, bestätigt sich im Umkehrschluss, dass eine neue Bewe‑ gung oder die Fortsetzung der bisherigen Trendphase begonnen hat. Investoren können Reverse Extensions zum Beispiel auch in langwierigen Seitwärtsphasen anlegen, um Fehlsignalen auf der Oberseite aus dem Weg zu gehen. Es wird erst in den Anstieg investiert, der in der Lage ist, die Reverse Extension der Seitwärtsbewegung oberhalb des Höchstkurses der Korrektur zu überschreiten. Ein Rückfall unter die untere Reverse Extension kann im Aufwärtstrend zum Signal für eine starke Gegenbewegung werden. In diesem Fall sollten die Stopps greifen.

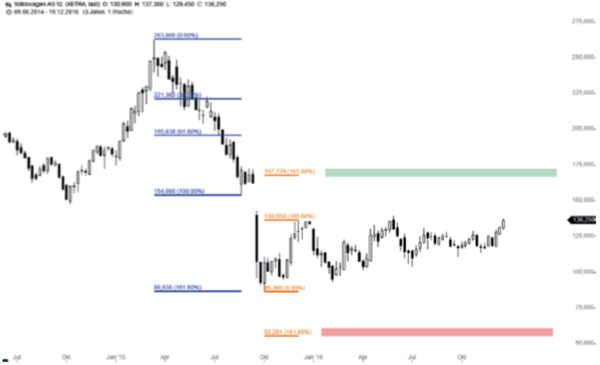
Man kann noch einen Schritt weiter gehen und auf der Basis der Korrekturen nicht nur Marken berechnen, die überschritten werden müssen, um die Trendfortsetzung zu bestätigen, auch konkrete Kursziele in Trendrichtung sind ableitbar: Für das Beispiel eines Abwärtstrends, der gerade korrigiert wird, bedeutet dies, dass man das Tool am höchsten Punkt der Erholung ansetzt und an den tiefsten Punkt der vorherigen Trendbewegung zieht. Damit werden die Extensionen in Trendrichtung bestimmt, die sich aus der maximalen Preisspanne der Korrektur ergeben . Ein Anwendungsfall ist gegeben, wenn der zugrunde liegende Trend eine sehr große Preisspanne umfasst und daher die ersten Extensionsniveaus sehr weit vom aktuellen Kurs entfernt wären (zum Beispiel bei Aktien, die einen starken Kurseinbruch verzeichneten und sich von diesem gerade erholen, vgl. Abbildung 24). So erhält man nähere und trotzdem valide Kursziele auf der Unterseite als die weit entfernten Extensionen einer gesamten Crashphase.

Abbildung 24: Reverse Extensions für den aktuellen Seitwärtstrend der VW-Aktie nach dem Einbruch im Rahmen des sogenannten »Abgasskandal-Crashs« (der an der 161,8-Prozent-Extension der ersten Abwärtstrendphase endete). Grün: Reverse Extension für mittelfristige Erholung, rot: Abwärtszielbereich für den Fall eines Einbruchs unter die bisherigen Tiefs.

Schlussgedanken: Fibonacci – Alles nur eine » Selffulfilling Prophecy«?

Der Erklärungsansatz ist so alt wie die Charttechnik. Je nachdem, ob man ihre Erfolge auf einfache Weise begründen und nachvollziehbar machen möchte oder ob man aus einer wirtschaftswissenschaftlichen Perspektive heraus Charttechnik in erster Linie für Humbug und Kaffeesatzleserei hält: Das häufigste Argument beziehungsweise der kritischste Einwand lautet in beiden Fällen, ihre positiven Ergebnisse an den Märkten seien die Folge einer »Selffulfilling Prophecy«. Der Begriff des Soziologen Robert K. Merton beschreibt das Phänomen, dass ein Ereignis durch das Verhalten einer Person oder Personengruppe herbeigeführt beziehungsweise erzeugt werden kann, die selbst an die Eintrittswahrscheinlichkeit des Ereignisses glaubt. So kann durch eigenes Verhalten ein Ereignis ausgelöst werden, das ursprünglich für das Ergebnis einer Handlung anderer Personen gehalten wurde.

DAuf die Börse umgemünzt bedeutet dies, dass eine Gruppe von Marktteilnehmern in einer bestimmten Situation oder an einer bestimmten Chartmarke das tut, was sie vom Markt erwartet, und diese Markterwartung tatsächlich ein‑ tritt, weil die Kursbewegung durch das Handeln der Gruppe selbst ausgelöst wurde. Nach diesem Muster soll erklärt werden, warum Fibonacci‑Marken Relevanz besitzen: Die Ursache ist schlicht die Gruppe der Fibonacci‑Trader, die diese Marken berechnet, dort handelt und damit dafür sorgt, dass an den Marken signifikante Kursbewegungen stattfinden.

Ist dieser Erklärungsansatz plausibel?

Eine solche Gruppe müsste beeindruckende Eigenschaften aufweisen: Sie bräuchte ein festes Regelwerk, das alle Fibonacci‑Trader anwenden, um auf die exakt gleichen Marken zu kommen. Das entsprechende Buch werden Sie im Internet vergeblich suchen. Die Trader müssten enorm gut vernetzt sein und ständig in konzertierten Aktionen Marktbewegungen anschieben oder abbremsen, damit »ihre« Marken erreicht werden. Sie müssten sich immer einig darüber sein, welche Marke, welches Retracement, welche Extension angelaufen werden soll. Sie müssten mit einer Unmenge an Kapital ausgestattet sein, um zum Beispiel an den großen Märkten ins Kursgeschehen lenkend eingreifen zu können, an denen die Methode ja ihre besten Ergebnisse liefert. Doch bei den marktbreiten Indizes oder am Devisenmarkt wären zig Millionen bis Milliarden Dollar, Euro etc. not‑ wendig, um entsprechende Marktbewegungen auszulösen oder zum Beispiel einen Trend bis zu einem bestimmten Punkt anzuschieben. Im Übrigen hätte es vor der Verbreitung der theoretischen Grundlagen keinerlei fibonaccispezifischen Bewegungsmuster, Verhältnisse oder Strukturen innerhalb von Kursverläufen geben dürfen. Doch Elliott und andere führten die Methode gerade deshalb ein, weil sie bereits vor knapp 100 Jahren auf ihre prognostische Aussagekraft gestoßen waren – und zwar durch die Betrachtung und Analyse von realen Kursverläufen. Aus meiner Sicht sollte man sich solchen Erklärungsversuchen mit der notwendigen Portion Skepsis nähern und das Phänomen ernst nehmen.

Die Treffsicherheit der Fibonacci‑Methode ist auf andere Charakteristika der Finanzmärkte zurückzuführen.

Die Märkte sind prinzipiell offen, die Vernetzung ist global, der Datenaustausch enorm schnell und Informationen sind leicht zugänglich. Die Geschwindigkeit, mit der man handeln oder auf Kursveränderungen reagieren kann, ist dank Internet und Digitalisierung der Finanzmärkte kaum mehr zu beschleunigen. Diese haben eine extrem hohe Zahl an Teilnehmern und das Maß an Interaktionen ist enorm – man betreibt schließlich Handel. Das Verhalten der Marktteilneh‑ mer ist zudem pfadabhängig, das heißt, für die Gründe von Kauf und Verkauf ist nicht nur der aktuelle Zustand, sondern genauso die (jüngere) Vergangenheit relevant. Damit haben die Finanzmärkte viele wesentliche Charaktereigenschaf‑ ten komplexer Systeme. Diese haben unter anderem die Eigenschaft, dass sie sich nichtlinear entwickeln, langfristige Prognosen über den Ablauf, die Form der Entwicklung oder die Definition von Zielen mit linearen Erklärungsansätzen nicht möglich sind und dass sie vor allen Dingen starke Wechselwirkungen und eine hohe (Eigen‑)Dynamik entfalten, die sich in sich verselbstständigenden Auf‑ schaukelungstendenzen widerspiegeln. Jedes System, jeder Schauplatz, an dem Menschen miteinander in dieser Weise vernetzt sind, kann daher exponentielle Entwicklungen vollziehen. Und je größer der Grad an Vernetzung, desto mehr Dynamik können diese Entwicklungen aufweisen. Hier greift die Hebb’sche Regel, die vom kanadischen Psychologen Donald O. Hebb 1949 aufgestellt wurde und aus der Forschung zu neuronalen Netzwerken stammt: Zellen, die miteinander Signale austauschen, vernetzen sich. »Neurons that fire together, wire together.« Und je besser sie vernetzt sind, desto schneller können sich Abhängig keiten, Rückkoppelungen und selbstverstärkende Prozesse entwickeln.

An der Börse kommt noch ein weiterer zentraler Aspekt hinzu, denn die Akteure haben ein gemeinsames Motiv: das Erzielen von Renditen.

Damit können auf der individuellen Entscheidungsebene äußere Faktoren zwar vor dem Investment eine tragende Rolle spielen. Ab dem Zeitpunkt der Investmentaktion beeinflusst jedoch die Kursentwicklung (und damit verbunden die Aussicht auf Gewinne beziehungsweise das Risiko, Verluste zu erleiden) die folgenden Entscheidungen des Anlegers. Da es sich an der Börse immer um  Prozesse handelt, also (Kurs‑)Veränderungen über die Zeit, haben die früheren und aktuellen Investmententscheidungen aller Marktteilnehmer über die Entwicklung der Kurse Einfluss auf die künftigen Urteile, Bewertungen und Entscheidungen aller Marktteilnehme.

Die Komplexität und der Wechsel von linearen zu nichtlinearen Wachstumsprozessen ist an der Börse nichts Neues. Man denke an die berühmte Tulpenmanie im Amsterdam des 17. Jahrhunderts, bei der die enormen Preissteigerungen von einem massiven Crash abgelöst wurden . Gleiches gilt für Aufstieg und Fall der Goldminen‑ und Eisenbahngesellschaften der USA zur vorigen Jahrhundertwende oder den Neuen Markt.

Crash und Rally sind aber nur die plakativen Extrembeispiele für die Abfolgen von Anstieg und Kursrückgang, Bewegung und Korrektur, die, beginnend auf den kleinsten Zeitebenen, tagtäglich eine komplexe Verlaufsstruktur gestalten, die nie gleich, aber immer ähnlich an den Börsen anzutreffen ist und sich bis in die größten Zeitebenen fortsetzt.

Wie geht man mit Komplexität um?

Wenn die Märkte diese Eigenschaften von Dynamik, Aufschaukelung und Komplexität haben, wenn der Beginn und der Ausgang von Entwicklungen nicht planbar und ihre Zukunft mittel‑ bis langfristig nicht prognostizierbar ist, wie kann man sich dann trotzdem zurechtfinden?

Das Zauberwort heißt Komplexitätsreduktion durch Musterbildung.

Man versucht, eine angemessene Vereinfachung des Systems durch  Abstraktion zu erreichen . Das ist eigentlich der Kern der Charttechnik. Die klassische Charttechnik greift sich aus dem gesamten Spektrum an Prozessvarianten im Kursverlauf diejenigen wiederkehrenden Strukturen heraus, die sie sehr klar erkennen und als Muster beschreiben kann (SKS, Dreiecke, Doppeltop, Trendkanal, Candlestickformationen etc). Und diese Vereinfachung führt dazu, dass man das Muster wiedererkennen und handeln kann.

Fibonacci‑Techniken vollziehen dagegen die Musterbildung auf Basis der Prozesse (Trendverhalten, Bewegung und Korrektur) und auf Basis des relativen prozentualen Vergleichs der preislichen oder zeitlichen Ausdehnung der Abläufe:

Man arbeitet nicht mit der absoluten Preisveränderung, sondern vermisst die Trends in Form von Relationen. Damit lässt man eine gewisse Unschärfe zu, weil man vereinheitlicht, statt sich mit allen Details der Kursverläufe auseinanderzusetzen.

Einfach gesagt: Der Methode reicht es aus, Anfang und Ende einer Bewegung zu kennen, um Aussagen zu treffen. Die Abfolge der Kurse innerhalb dieser beiden Punkte findet nur dann Beachtung, wenn ein zuvor definiertes Fibonacci‑Level durchschritten wird.

Die Fibonacci‑Analyse trennt dabei methodisch die Prozesse, die Wachstum und zeitlich begrenzte Aufschaukelungstendenzen theoretisch nach sich ziehen können (Bewegungen), von denen, die dazu nicht in der Lage sind und denen eine Phase der Stagnation (Korrektur) folgt. Das Unterscheidungskriterium ist das Verhalten der Gegenbewegung, also die Frage, ob eine Handelsstrecke 61,8 Prozent retraced wird oder nicht. Prozesse, die weniger als 61,8 Prozent korrigiert werden, müssen nicht zwangsläufig in eine Trendphase mit exponentiellem oder ungebremstem Kurswachstum münden. Aber sie haben das Potenzial dazu . Während den anderen, mehr als 61,8 Prozent retraceten Spannen dieses Potenzial fehlt. Das ist zugleich die Basis und das Erfolgsgeheimnis der Methode.

Sie konzentriert sich damit nicht auf die Details der einzelnen Abläufe, sondern auf deren Rahmenbedingungen. Für trendbestätigende, trendunterbrechende, trendbeendende Entwicklungen werden diese Bedingungen aus der Beobachtung heraus formuliert und in Analyse und Trading umgesetzt. Daher können die Werkzeuge bei kleinen, wenige Euro reichenden Intradaytrends ebenso genutzt werden wie in jahrelangen Trendphasen, die zum Beispiel zur Vervielfachung einer Aktie führen.

Das bedeutet nicht, dass man ausgehend von einer Trendphase den genauen zukünftigen Verlauf oder den exakten Endpunkt der künftigen Kursentwicklung vorherbestimmen kann . Aber man kann aus dem Verlauf Potenziale ableiten, die unter der Bedingung, dass sich der Trend fortsetzt, peu à peu abgearbeitet werden . Und nachdem alle Varianten von Bewegung und Korrektur in Aufwärts‑, Abwärts‑ und Seitwärtsmärkten, auf allen Zeitebenen und bei jedem Basiswert auftreten, hat man ein passendes Schema, das universell eingesetzt werden kann.

Dabei sind die Fibonacci‑Methode und ihre benachbarten Theoriezweige vielleicht noch nicht der Weisheit letzter Schluss. Vielleicht kommen in Zukunft weitere Erklärungsmodelle und Theorien ins Spiel, die dem Wesen der Märkte tiefer auf den Grund gehen. Aber sie ist eine Vorgehensweise, welche die Komplexität, die Wachstumsprozesse und selbstverstärkenden Wechselwirkungen an den Märkten schon sehr genau im Chart erfassen kann: Jede Bewegung der jüngeren Vergangenheit hängt mit den ihr vorangegangen zusammen. Die Entwicklung der früheren Bewegungen bestimmt das Potenzial der aktuellen und der künftigen mit: 1+1 = 2, 2+1 = 3, 2+3 = 5.

Bullen und Bären können also eine Menge von Kaninchen lernen.

Lesen Sie auch...

Fibonacci-Analyse und -Trading (Thomas May 1)

Fibonacci — Berechnung von Retracements (Thomas May 2)

Fibonacci — Berechnung von Extensionen (Thomas May 3)

Fibonacci — Umsetzung in die Praxis (Thomas May 4)

Fibonacci in der Diagonale: Trendlinien, Fans und Fibonacci-Matrix (Thomas May 5)

Fibonacci — Anwendung der Fibonacci-Methode im Trading (Teil 1, Thomas May 6)

Fibonacci — Anwendung der Fibonacci-Methode im Trading (Teil 2, Thomas May 7)