Die Welt der automatisierten Handelssysteme ermöglicht es Ihnen, chartanalytische Handelssysteme zu erstellen, die genau nach Ihren Vorstellungen arbeiten. Welche Tücken kann ein solches automatisiertes Handelssystem haben, welche Fallen lauern bei der Programmierung und wo liegen die Vor- und Nachteile der verschiedenen Systeme? Alle diese Fragen beantwortet Ihnen der Autor Uwe Gresser in diesem Buch.

Der Herausgeber dieses Buches schreibt: Die Bestimmung des Risikos in einem Portfolio ist nicht so einfach. In der Regel sind die Renditeausprägungen der einzelnen Wertpapiere nicht völlig gleichgerichtet. Beispielsweise kann der in einem Investment erlittene Verlust durch den Gewinn in einem anderen Investment teilweise oder gänzlich kompensiert werden. Zur Bestimmung des Portfoliorisikos müssen zunächst die Kovarianz sowie der Korrelationskoeffizient ermittelt werden.

Kaufen Sie dieses Buch über FinanzBuchVerlag

Möchten Sie Ihre Techische Analyse üben? Testen Sie eine kostenlose Trading-Plattform Demo

Wir haben die Sondergenehmigung erhalten, einen ausführlichen Auszug aus diesem Buch zu veröffentlichen. Nachfolgend stellen wir Ihnen das erste Kapitel vor, in dem die Portfoliotheorie nach Markowitz behandelt wird.

1. Einsatz des automatisierten Handelssystems Gresser K9 im Portfoliomanagement

Portfoliotheorie nach Markowitz

Risiko- und Renditequantifizierung eines Wertpapiers
Die klassische Portfoliotheorie basiert auf den Betrachtungen von Harry M. Markowitz. Er geht zunächst von folgenden zentralen Prämissen aus:

• Ein Investor verhält sich bei einer Anlageentscheidung risikoscheu. Der Grad der Risikoaversion ist individuell unterschiedlich.
• Der Anleger handelt rational und nutzenmaximierend.
• Jede Anlagealternative wird nicht nur auf ihre Renditechance, sondern auch auf ihr Verlustpotenzial untersucht.
• Der Kapitalmarkt ist vollkommen.

Ziel der Portfoliotheorie ist es, durch geschickte Wahl der Anlagen eine Diversifikation im gesamten Portfolio des Anlegers zu erreichen. Es soll dabei das Risiko im Gesamtportfolio bei gleicher Rendite geringer sein als in einer Einzelanlage. Im folgenden Kapitel soll die Ermittlung eines theoretisch optimalen Portfolios untersucht werden.

Um Anlagen unterschiedlicher Natur vergleichbar zu machen, sind Messgrößen zur Ermittlung von Risiken und Renditechancen eingeführt worden. Diese Ertragsaussichten können als Zufallsvariablen angenommen werden, deren Realisation von verschiedenen zukünftigen Umweltzuständen – zum Beispiel Zins-und Konjunkturentwicklungen – abhängt. Im nächsten Schritt werden diesen prognostizierten Szenarien spezifische Eintrittswahrscheinlichkeiten zugeordnet. Anschließend erfolgt eine Schätzung der durch die Szenarien hervorgerufenen Renditeausprägungen der untersuchten Wertpapiere.

Der Erwartungswert der zukünftigen Rendite eines Wertpapiers berechnet sich nach der Formel:

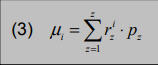
μ_i = erwartete Rendite des Wertpapiers i
p_z = Eintrittswahrscheinlichkeit von z
rⁱ_z = Rendite des Wertpapiersibei Eintritt von z
z = Umweltzustand

wobei die Summe aller Eintrittswahrscheinlichkeiten gleich 1 sein muss:

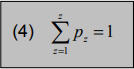
Der Erwartungswert ergibt sich somit aus der Summe der mit den jeweiligen Eintrittswahrscheinlichkeiten gewichteten entsprechenden Renditeausprägungen. Er ist eine erste Messgröße, um verschiedene Wertpapiere bezüglich ihrer Renditeerwartungen miteinander zu vergleichen. Allerdings fehlt – den Grundprämissen folgend – eine Aussage über die jeweiligen Risiken. Diese lassen sich über die abweichenden Schwankungen der Renditen vom Erwartungswert ermitteln. Dabei findet die Varianz Anwendung, um das Risiko einer Investition abzubilden:

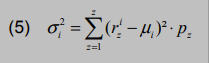
σ_i² = Varianz des Wertpapiers i

Da die Dimension der Varianz nicht mit der des Erwartungswertes übereinstimmt, wird die Standardabweichung berechnet, die als Volatilitätsmaß – und damit als Risikomaß – betrachtet werden kann. Sie berechnet sich wie folgt:
Die Standardabweichung beschreibt die durchschnittliche Abweichung der Rendite vom Erwartungswert eines Wertpapiers.

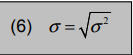
Eine isolierte Betrachtung der Rendite beziehungsweise eine isolierte Betrachtung des Risikos eines Wertpapiers führen zu keinem aussagekräftigen Ergebnis, welche Anlagealternative für den Investor die günstigere ist. Eine Kombination der Messgrößen führt jedoch zu indifferenten Aussagen, wie in der folgenden Tabelle für zwei fiktive Wertpapiere dargestellt wird:

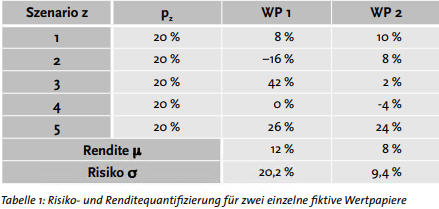
Risiko- und Renditequantifizierung eines Portfolios

Da aus dem vorigen Abschnitt die Betrachtung von Rendite und Risiko keine eindeutige Entscheidung für das eine oder das andere Wertpapier hervorgebracht hat, soll nun die Rendite- und Risikoquantifizierung für ein Portfolio bestimmt werden. Dabei wird in diesem Zusammenhang unter einem Portfolio der Bestand von zwei oder mehreren Wertpapieren im Depot eines Anlegers verstanden. Das Vermögen eines Investors wird dementsprechend auf mehrere Anlagen aufgeteilt. Die erwartete Gesamtrendite eines solchen Portfolios setzt sich aus den Renditen der einzelnen Wertpapiere und ihrer Gewichtung im Portfolio zusammen.

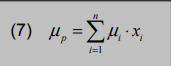
μ_p = erwartete Rendite eines Portfolios
x_i = Anteil des Wertpapiersiam Portfolio

wobei auch hier gilt, dass die Summe der Anteile aller Wertpapiere1ergeben muss.

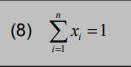
Die Bestimmung des Risikos gestaltet sich jedoch nicht so einfach. Eine schlichte Addition der gewichteten Risiken reicht dazu bei weitem nicht aus. In der Regel sind die Renditeausprägungen der einzelnen Wertpapiere nicht völlig gleichgerichtet. Beispielsweise kann der in einem Investment erlittene Verlust durch den Gewinn in einem anderen Investment teilweise oder gänzlich kompensiert werden. Zur Bestimmung des Portfoliorisikos müssen zunächst die Kovarianz sowie der Korrelationskoeffizient ermittelt werden.

Die Kovarianz ist ein Maß für den Gleichlauf zweier Renditen und berechnet sich nach folgender Formel:

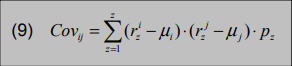
Cov_ij= Kovarianz
μ_i = erwartete Rendite des WP i
μ_j = erwartete Rendite des WP j

Da sich aus der Kovarianz nur schwer ein Ergebnis ablesen lässt, inwieweit sich die Renditen zweier Anlagen ähnlich verhalten, wird die Kovarianz durch das Produkt der jeweiligen Standardabweichungen dividiert, wodurch der Korrelationskoeffizient ermittelt wird.

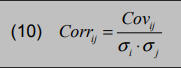
Corr_ij = Korrelationskoeffizient zwischen WP i und j –1 ≤ Corr_ij ≤ + 1

Die Korrelation stellt den Gleichlauf zwischen zwei Wertpapieren normiert dar. Sie schwankt zwischen den Extremwerten –1 und +1, wobei –1 eine ideale negative Korrelation – die beiden Anlagen verhalten sich völlig gegensätzlich – und +1 eine ideale positive Korrelation – die beiden Anlagen verhalten sich völlig gleich – aufweisen. Bei einer Korrelation von Null ist kein zusammenhängendes Verhalten zwischen den beiden Renditen zu erkennen. Die Bildung eines Portfolios ist immer dann vorteilhaft, wenn die Renditen der Wertpapiere nicht vollständig positiv zueinander korrelieren. Das Augenmerk einer Diversifikation liegt darin, dass das Risiko der gehaltenen Wertpapiere verringert wird, ohne dass dabei bei der Renditeerwartung ein zu großer Kompromiss eingegangen werden muss.

Mithilfe der Kovarianz beziehungsweise des Korrelationskoeffizienten lässt sich nun das Portfoliorisiko bestimmen:

Kaufen Sie dieses Buch über FinanzBuchVerlag

Leute lesen auch

• Jens Klatt – Trader - Der Weg zur profitablen Handelsstrategie
• Wilhelm Eder: Traden nach Plan – So entwickeln Sie einen systematischen Handel
• Van K. Tharp – Clever traden mit System 2.0