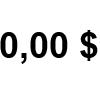Bo Yoder ist ein international anerkannter und viel beachteter Trading-Coach. Seiner Meinung nach findet die beste Absicherung einer Spekulation im Kopf des Anlegers statt - und dieser Ansatz wird dem Leser anhand zahlreicher praktischer Beispiele aus der Welt der "Trading-Psychologie" auf unterhaltsame Weise nahe gebracht. Des Weiteren erklärt dieser Leitfaden klar und verständlich, wie man mit sorgfältiger Analyse seine Gewinne erhöht, Drawdowns reduziert, strategische Fehler vermeidet und ein Gespür für das richtige Timing beim Trading entwickelt. 

Er schreibt die folgende Aussage: Das Ziel dieses Buchs ist jedoch, Ihren Vorteil auf den Finanzmärkten dieser Welt zu optimieren. Die organischen Einheiten zeigen ständige Veränderungen in Reaktion auf Emotionen, wirtschaftlichen Druck und gesellschaftliche sowie kulturelle Verschiebungen. Die Veränderung ist die einzige Konstante, und manchmal fällt es schwer, Regeln zu identifizieren.

Kaufen Sie dieses Buch über FinanzBuchVerlag

Möchten Sie Ihre Techische Analyse üben? Testen Sie eine kostenlose Trading-Plattform Demo

Wir haben die Sondergenehmigung erhalten, einen ausführlichen Auszug aus dem ersten Kapitel dieses Buches zu veröffentlichen. Eine angenehme Lektüre wünschen wir Ihnen.

KAPITEL 1
WAS IST DER „VORTEIL?”

Der Vorteil des Gewinners liegt nicht in einer vorteilhaften Geburt, einem
hohen IQ oder Talent. Den Vorteil des Gewinners macht die Einstellung aus,
nicht die Fähigkeit. Die Einstellung ist das entscheidende Erfolgskriterium.
- DENIS WAITLEY

Der Mensch ist ein Lebewesen, das dazu geschaffen ist, aggressiv Risiken einzugehen. Unsere frühen Vorfahren haben auch Glücksspiele erfunden, wenn sie nicht gerade in einer gefährlichen Welt ihre persönliche Sicherheit riskierten. Es gibt Beweise, dass Glücksspiele schon vor mehr als 4000 Jahren in den antiken Zivilisationen Chinas, Ägyptens und Roms verbreitet waren.

Diese antiken Glücksspiele wurden oft mit einem würfelförmigen Knochen gespielt, der aus den Knöcheln von Schafen oder Hirschen gewonnen wurde. Später stellte man handwerklich gefertigte Würfel aus Elfenbein oder Stein her. In Ägypten fand man einen Satz Elfenbeinwürfel, die etwa aus der Zeit um 1500 v. Chr. stammen, und um 900 v. Chr. stellten die Etrusker Würfel mit Ziffern her, die auch jedem Casinoangestellten in Las Vegas bekannt vorkommen würden.

In der Antike gehörten Glücksspiele zum großen Teil zu den abergläubischen und religiösen Erfahrungen der damaligen Zivilisationen. Die Wahrscheinlichkeitstheorie und die Mathematik waren noch nicht entwickelt, und daher glaubten die Zocker der Antike tatsächlich, dass die Götter selbst das Ergebnis jedes einzelnen Wurfes beim Würfeln kontrollierten. Heute würde wohl fast jeder Mensch verstehen, dass diese antiken Glücksspiele reines Zocken waren, ohne jede Veränderung der statistischen Wahrscheinlichkeiten außer solchen, die durch fehlerhafte Würfel verursacht wurden. Da die Regeln des Spiels zu einem einfachen Gewinn oder Verlust führten, ähnlich wie beim Werfen einer Münze, wurde das Ergebnis nach einer langen Nacht des Zockens durch die Mechaniken des Spiels bestimmt, nicht durch die Mathematik der Auszahlungsstruktur.  Daher beginnt unsere Untersuchung des Vorteils auch nicht im alten Ägypten, sondern in Pavia, Italien, im Jahr 1560.

DIE REGELN DES GLÜCKSSPIELS

Gerolamo Cardano war Mathematiker, Physiker, Astrologe und vor allem Glücksspieler in der Zeit der italienischen Renaissance. Cardano war ein Freund Leonardo da Vincis und ist heute vor allem für seine Leistungen auf dem Gebiet der Algebra bekannt. In den 1560er-Jahren schrieb er ein Buch mit dem Titel Liber de Ludo Aleae (Buch über das Würfelspiel), aber veröffentlicht wurde es erst nach seinem Tod 1663. Liber de Ludo Aleae gilt als erstes Buch über die systematische Behandlung der Wahrscheinlichkeit in Bezug auf Glücksspiele. In diesem Buch legt Cardano die Grundlagen der Wahrscheinlichkeiten beim Würfelspiel dar, die für uns alle heute selbstverständlich sind. Indem er die Frage „Wie hoch ist die Wahrscheinlichkeit, dass ich beim nächsten Mal eine Zwei würfle?” mathematisch beantwortete, war Cardano der Erste, der das Resultat des Würfelspiels als etwas anderes als den Willen der Götter erforschte.

Die Veränderung des Denkens scheint eine einfache Sache zu sein, aber sie hatte tief greifende Auswirkungen. Sehen Sie sich das einmal aus der Perspektive eines Glücksspielers im 17. Jahrhundert an: Sobald Sie verstanden haben, dass nicht die Götter das Ergebnis jedes einzelnen Wurfes bestimmen, kann man die Möglichkeit studieren und verstehen, dass man das Ergebnis auf Basis der Spielregeln exakt vorhersagen kann. Wenn die Regeln einen der Spieler bevorzugen, dann hat diese Person einen statistischen Vorteil gegenüber ihren Opponenten.

Das bringt uns zu den folgenden Definitionen und ihren Prinzipien:

Ein faires Spiel, etwa ein Münzwurf mit einem Einsatz von einem Dollar pro Wurf, bietet keinem Spieler einen statistischen Vorteil. Kurzfristig kann ein Spieler von einer vorübergehenden statistischen Anomalie profitieren, die eine „Glückssträhne” liefert. Aber auf lange Sicht werden beide Spieler genau da landen, wo sie begonnen haben. Die Wahrscheinlichkeit, dass ein bestimmter Spieler beim nächsten Münzwurf gewinnen wird, liegt bei 50 Prozent. Die Wahrscheinlichkeit eines Verlusts beträgt ebenfalls 50 Prozent. 

Ein Spiel mit einem Vorteil dagegen bevorzugt einen der Spieler in statistischer Hinsicht. Dieser Vorteil kann offensichtlich sein (bei 1, 2, 3 und 4  gewinne ich, bei 5 und 6 gewinnt der Gegner) oder auf Mathematik basieren (bei Kopf gewinne ich zwei Dollar, bei Zahl verliere ich einen Dollar).

Sehen Sie sich als Beispiel für dieses Prinzip das folgende Spiel mit einem Vorteil an: Sie fordern einen Gegner heraus, einen Würfel zu rollen und das Ergebnis korrekt vorherzusagen. Sie bieten ihm an, ihm für jede richtige Prognose vier Dollar zu zahlen, er muss Ihnen bei jeder falschen Prognose einen Dollar geben.

Obwohl die hohe Auszahlung beim Einsatz auf den ersten Blick attraktiv wirkt, bevorzugen Sie die Spielregeln ganz enorm. Je länger Sie das Spiel nach diesen Regeln spielen, desto höher ist der Gewinn, den Sie erwarten dürfen. Da das Ergebnis durch ein mechanisches Wahrscheinlichkeitssystem bestimmt wird (ein Würfel mit sechs Seiten), kann man den exakten Vorteil berechnen, indem man alle möglichen Ergebnisse des Spiels auf logische Art und Weise durchdenkt.

Wir wissen, dass der Würfel sechs Seiten hat, und daher liegt die Wahrscheinlichkeit für jede einzelne Prognose bei eins zu sechs. Nach den Regeln des Spiels zeigt eine der Würfelseiten die Zahl, die Ihr Gegner genannt hat, was für Sie zu einem Verlust von vier Dollar führt. Die Wahrscheinlichkeit, dass dies geschieht, beträgt bei jedem einzelnen Wurf 16,66 Prozent (1/6). Fünf der sechs Seiten führen jedoch zu einem Verlust Ihres Gegners und für Sie zu einem Gewinn von einem Dollar. Die Wahrscheinlichkeit, dass dies geschieht, liegt für jeden einzelnen Wurf bei 83,33 Prozent (5/6).

Wenn Sie das Spiel nur einmal spielen, verlieren Sie mit einer Wahrscheinlichkeit von 16,66 Prozent vier Dollar. Je länger Sie aber spielen, desto mehr wird sich das Ergebnis der statistischen Wahrscheinlichkeit annähern. Nach 100 Würfen dürfen Sie damit rechnen, den Einsatz von einem Dollar 83 Mal gewonnen zu haben, was einem Profit von 83 Dollar entspricht. Ihr Gegner darf damit rechnen, bei 17 der 100 Durchgänge vier Dollar von Ihnen zu erhalten, insgesamt also 68 Dollar. Wenn Sie die Summe von Ihren Gewinnen abziehen, verbleibt Ihnen ein Nettogewinn von 15 Dollar. Diese 15 Dollar Profit sind das Ergebnis Ihres Vorteils bei diesem speziellen Spiel. In Prozentsätzen ausgedrückt, sollte das Spiel dem bevorzugten Spieler für jeden eingesetzten Dollar einen Gewinn von 15 Prozent einbringen.

Wenn Ihr Opponent regelmäßig einen Dollar einsetzt, dann liegt ihre statistisch ausgedrückte Gewinnerwartung bei 15 Cent je Spieldurchgang. Wenn ein neuer Gegner von diesem Spiel hört, daran teilnehmen und bei jedem Durchgang 100 Dollar einsetzen will, liegt Ihre statistische Gewinnerwartung pro Wurf bei 15 Dollar! Da Sie das Potenzial erkennen, das Ihnen dieser Vorteil bietet, laden Sie am nächsten Abend zehn Spieler in Ihr Haus ein. Alle kommen wie geplant, und jeder beginnt den Abend mit Einsätzen von 20 Dollar je Durchgang. Das bedeutet, dass jedesmal 200 Dollar eingesetzt werden. Bei einem statistischen Vorteil von 15 Prozent bedeutet es, dass auf Dauer mit jedem Durchgang 30 Dollar in Ihre Taschen fließen. Wenn es pro Stunde 100 Durchgänge gibt, sollten Sie pro Stunde ungefähr 3000 Dollar verdienen!

DIE MACHT DES STATISTISCHEN VORTEILS

Die Macht dieser Art von statistischem Vorteil ist der Grund, warum Casinobetreiber in Las Vegas eine Milliarde Dollar für den Bau eines prächtigen Casinos ausgeben können, um Gäste anzulocken. Sie sollen dort Glücksspiele spielen, bei denen das Casino einen statistischen Vorteil hat. Um die Macht eines statistischen Vorteils besser zu verstehen, wollen wir ihn am Beispiel eines Roulettetischs analysieren.

Ein amerikanisches Rouletterad hat 38 nummerierte Felder. Jeder Spieler legt seine Einsätze auf den Tisch und versucht das Ergebnis des nächsten Durchgangs vorherzusagen. Die Spieler können auf einzelne Zahlen setzen (1 bis 36), auf Zahlenkombinationen oder einfach auf Rot oder Schwarz (18 Zahlen sind rot und 18 sind schwarz). Obwohl die Regeln und die Auszahlungen kompliziert erscheinen können, gibt es einen einfachen Grund dafür, dass das Casino am Roulettetisch einen massiven Vorteil genießt ... zwei der Fehler tragen die Zahl 0! Wenn die Kugel auf einem dieser beiden Felder landet, sind alle Standardwetten verloren und das „Haus” streicht einen hohen Gewinn ein.

Die einfachste Wette wäre, dass die Kugel bei der nächsten Drehung des Rads entweder auf Rot oder auf Schwarz landet. Wenn Sie zehn Dollar auf Rot setzen, dann gibt es 18 Felder, die Ihnen einen Gewinn bringen sowie 18 schwarze Felder plus die beiden 0-Felder, insgesamt also 20, mit denen Sie einen Verlust von zehn Dollar erleiden. Wenn wir Cardanos Wahrscheinlichkeitsstudien auf diese Spielregeln anwenden, dann bemerken wir, dass sie fair wären, wenn es die 0-Felder nicht gäbe. Dann nämlich könnten wir erwarten, dass die Kugel in 50 Prozent aller Fälle auf einem Feld mit der richtigen Farbe landet. Es gibt aber bei jedem Durchgang eine Wahrscheinlichkeit von 5,26 Prozent (zwei von 38 Feldern), dass der Ball auf einem 0-Feld landet, und das verschiebt die Wahrscheinlichkeit zugunsten des Casinos. Bei einem statistischen Vorteil von 5,26 Prozent darf das Casino einen Gewinn von 5,26 Dollar je 100 Dollar Einsatz erwarten. Da das Rouletterad in einem Casino in Las Vegas etwa 45 Mal pro Stunde gedreht wird, können Sie leicht erkennen, wie schnell sich die Gewinne addieren.

Die Vorteile der Casinos bei den verbreitetsten Glücksspielen sind oft recht ansehnlich. Daher kann man sie mit extremer Genauigkeit schätzen und vorhersagen, wenn die Zahl der Einzelfälle (Durchgänge des Spiels) hoch genug ist. Deshalb sieht man in einem typischen Spielcasino auch so viele Tische. Gäbe es dort nur einen Tisch, dann würde das Casino unter dem typischen Auf und Ab der natürlichen Varianz seines Vorteils leiden. Wenn der Casinobetreiber aber zehn Tische hat, oder noch besser 100 in verschiedenen Gebäuden, dann gibt das Gesetz der großen Zahl dem Casinobetreiber quasi eine Garantie auf den Vorteil von 5,26 Prozent.

GRUNDSÄTZLICHES ÜBER WAHRSCHEINLICHKEIT

Das Gesetz der großen Zahlen gehört zu den fundamentalen Theorien der Wahrscheinlichkeit. Es besagt: Wenn die Zahl der Einzelfälle oder der voneinander unabhängigen Wiederholungen wächst, dann kommt der Durchschnittswert der Ergebnisse der statistischen Prognose des wahrscheinlichen Ergebnisses immer näher. Einfacher ausgedrückt: Je höher die Grundgesamtheit (die Zahl der Einzelfälle), desto höher ist die Wahrscheinlichkeit, dass das Resultat jedes zufälligen Ereignisses die statistische Wahrscheinlichkeit seines Auftretens erreicht. Diese Theorie wurde erstmals Ende des 15. Jahrhunderts vom Schweizer Mathematiker Jacob Bernoulli beschrieben. Sein postum 1713 erschienenes Buch Ars Conjectandi (Die Kunst der Mutmaßung) gilt als eins der grundlegenden Dokumente der mathematischen Wahrscheinlichkeitsrechnung.

Zum Beweis des Gesetzes der großen Zahlen oder Bernoullis Theorem kann man sich die Wahrscheinlichkeit beim Würfelspiel ansehen. Da ein Würfel sechs Seiten hat, besteht bei jedem einzelnen Wurf eine Chance von eins zu sechs, dass die Zahl 5 gewürfelt wird. Die statistische Wahrscheinlichkeit ist absolut, aber die Wahrscheinlichkeit, dass bei sechs Würfen jeweils einmal die 5 resultiert, ist nicht so hoch. Nur wenn die Zahl der Durchgänge groß genug ist, dürfen wir stark darauf vertrauen, dass die 5 in einem Sechstel aller Versuche gewürfelt wird.

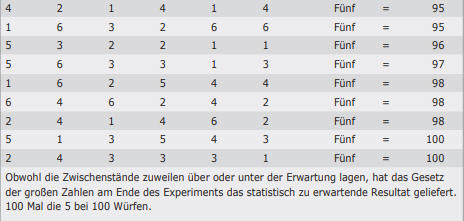
Eine Versuchsreihe führt visuell vor Augen, wie das Gesetz der großen Zahlen funktioniert. Besorgen Sie sich sechs Würfel. Rollen Sie diese 100 Mal und notieren Sie sich, wie oft die 5 auftaucht. Statistisch gesehen sollte das bei jedem Wurf mit sechs Würfeln einmal der Fall sein. Sie sollte bei zehn Würfen zehn Mal und bei 100 Würfen 100 Mal auftauchen. Im Glauben an das Gesetz der großen Zahlen bin ich nicht zuversichtlich, dass die 5 beim ersten Wurf auftaucht, einigermaßen zuversichtlich, dass sie bei zehn Würfen ungefähr zehn Mal und extrem zuversichtlich, dass sie am Ende des Experiments 100 Mal aufgetaucht sein wird.

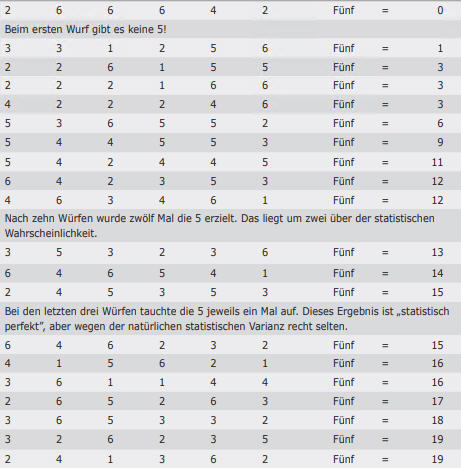
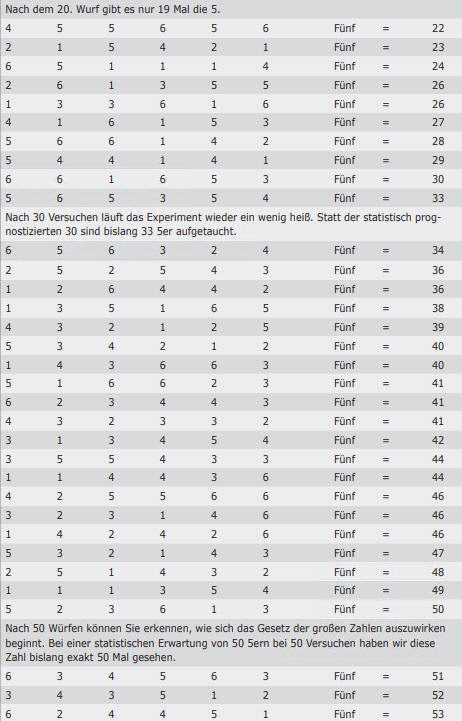
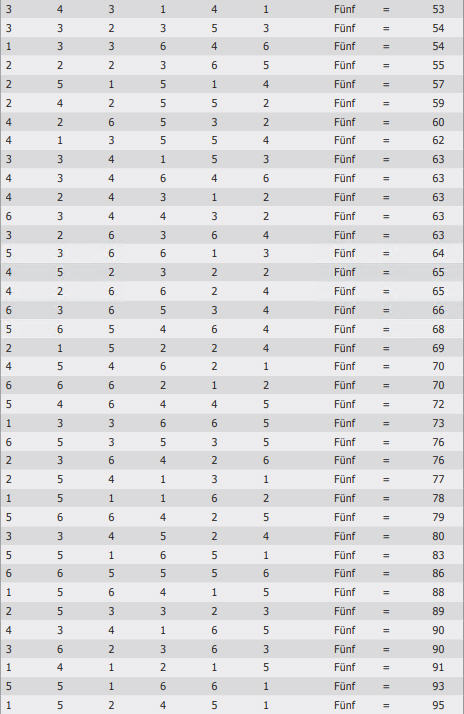
OPTIMIEREN SIE IHREN STATISTISCHEN VORTEIL

Man kann das Konzept des Vorteils gut anhand von Glücksspielen illustrieren, weil diese Spiele von Natur aus mechanisch sind. Ein sechsseitiger Würfel ist, was er ist. Er hat eine bestimmte Zahl von Seiten und wird seit 4000 Jahren auf die gleiche Weise konstruiert. Das macht die Vorteilsanalyse zu einer einfachen mathematischen Übung.

Das Ziel dieses Buchs ist jedoch, Ihren Vorteil auf den Finanzmärkten dieser Welt zu optimieren. Die organischen Einheiten zeigen ständige Veränderungen in Reaktion auf Emotionen, wirtschaftlichen Druck und gesellschaftliche sowie kulturelle Verschiebungen. Die Veränderung ist die einzige Konstante, und manchmal fällt es schwer, Regeln zu identifizieren. Wenn der Vorteil des Casinos in diesem Spektrum das eine Extrem an Klarheit darstellt, besetzen die Finanzmärkte das andere. Zum besseren Verständnis der Verbindungen zwischen den beiden wollen wir nun ein auf statistischen Vorteilen basierendes Geschäft betrachten, das zwischen den beiden Extremen liegt.

Muster und Modellbildung

Wenn Sie einen Moment darüber nachdenken, dann ist eine Versicherungspolice im Grunde genommen eine simple Wette. Sie vermuten nicht, dass Sie in den kommenden drei Monaten in einen Autounfall verwickelt sein werden, aber andererseits könnte ein solcher Unfall Ihren Finanzen und /oder Ihrer Gesundheit extremen Schaden zufügen. Dieses Risiko wollen Sie nicht auf sich nehmen. Daher schließen Sie mit einem Versicherungsunternehmen eine strukturierte finanzielle Wette ab. Sie wetten eine bestimmte Summe darauf, dass Sie in einen Autounfall verwickelt sein werden, und das Unternehmen hält dagegen. Um den richtigen Preis für Ihre Police zu ermitteln, verwendet die Versicherung statistische Muster und Modelle, um mit relativer Genauigkeit die Wahrscheinlichkeit der Katastrophe prognostizieren zu können. Sie kann das nicht deshalb, weil sie irgendetwas über Ihren Fahrstil oder Ihr Können am Lenkrad weiß. Aber weil sie genug Fahrer versichert, stellt das Gesetz der großen Zahlen sicher, dass die Ergebnisse ihren statistischen Modellen recht genau entsprechen werden. Eine bestimmte Zahl von Fahrern aus Ihrer demografischen Gruppe wird in Unfälle verwickelt sein, und die Höhe ihrer Ansprüche wird im Schnitt in der Nähe der prognostizierten Summe liegen. Diese Verluste werden von den Versicherungsprämien der anderen Kunden mehr als ausgeglichen, und die Differenz zwischen beiden Summen ist der Quartalsgewinn des Versicherungsunternehmens.

Wie in den vorherigen Beispielen schon gezeigt wurde, ist der statistische Vorteil eine Funktion der Wahrscheinlichkeit eines Verlustereignisses gegenüber seiner positiven Gewinn-Verlust-Relation. Ein faires Spiel wie ein Münzwurf oder das Setzen auf Rot am Roulettetisch kann zu einer von einem Vorteil geprägten Situation werden, wenn man die Wahrscheinlichkeiten verändert – wenn man also zum Beispiel zwei Verlustfelder auf dem Rouletterad hinzufügt oder die Auszahlungsregeln modifiziert. Wenn ich Ihnen die Chance anbiete, bei einem Münzwurf 100 Dollar einzusetzen, könnten Sie dieses faire Spiel akzeptieren, falls Sie unterhaltsame Glücksspiele mögen. Wenn Ihnen aber jemand beim gleichen Münzwurf eine Gewinnwahrscheinlichkeit von zwei zu eins anböte, dann würden Sie zum nächsten Geldautomaten eilen und das Tagesmaximum abheben, weil Ihr statistischer Vorteil bei dieser Auszahlungsregel enorm wäre.

Genau diese Formel analysiert das Versicherungsunternehmen, wenn es Ihre Police ausstellt. Es sieht sich Ihre Unfallbilanz und auch die der anderen Fahrer in Ihrer demografischen Gruppe an, um die Wahrscheinlichkeit zu ermitteln, dass Sie in einen Unfall verwickelt sein werden. Sobald diese Wahrscheinlichkeit definiert ist, kann die Versicherung bestimmen, wie das Rendite-Risiko-Verhältnis aussehen muss, um ihr langfristig einen Profit zu sichern. Die Versicherungsbranche kalkuliert mit winzigen Wahrscheinlichkeiten. Daher kann sie auch mit einem stark inversen Rendite-Risiko-Verhältnis in ihren Policen profitabel existieren. Die Versicherer wissen, dass sie einige hohe Auszahlungen leisten müssen, wenn Kunden an Unfällen beteiligt sind. Aber wenn ihre ursprüngliche Risikoanalyse korrekt war, dann decken die Tausende von kleinen Prämien, die sie jeden Monat einnehmen, diese Verluste mehr als ab.

GEWINNERWARTUNGEN

Immer wenn Sie auf den Finanzmärkten dieser Welt ein Investment oder einen Trade vornehmen, versichern Sie im Grunde genommen einen anderen Trader gegen einen Verlust. Wenn Sie eine Aktie in einem Aufwärtstrend kaufen, weil Sie annehmen, dass sich der Trend fortsetzen wird, dann ist der Verkäufer der Aktien gegenteiliger Meinung und tritt Ihnen sein Recht auf künftige Gewinne ab. Dafür eliminieren Sie durch den Kauf sein Risiko. Sie übernehmen das Risiko eines Verlusts mit den gekauften Aktien für das Recht, eventuelle künftige Gewinne einzustreichen. Diese Meinungsverschiedenheit (der eine Trader übernimmt ein seiner Meinung nach „gutes” Risiko, der andere entledigt sich eines seiner Meinung nach „schlechten” Risikos) ist die grundlegende Gewinnquelle auf jedem Finanzmarkt. Machen Sie sich keine Illusionen: Trading ist ein Nullsummenspiel. Wenn Sie einen Gewinn realisieren wollen, muss ein anderer Trader eine Fehlentscheidung treffen und Ihnen sein Risiko in einer Position des Nachteils verkaufen. Seine vergebene Chance oder sein Kapitalverlust wird zu Ihrem Gewinn.

Lektionen vom Poker

Weil es bei der Finanzspekulation keine spezifische Struktur und keine festen Regeln gibt, muss jeder Trader selbst entscheiden, wie er seine Methode der Trendanalyse strukturieren will. Eines der wenigen Glücksspiele, welches die gleiche Wahlfreiheit bietet, ist Poker, und man kann von diesem populären Kartenspiel viel für das Trading lernen. Es gibt zwar rigide Regeln, was die Wertigkeit der Kartenkombinationen („hands”), die Bieterrunden und das Austeilen der Karten betrifft, aber abgesehen davon bietet Poker enorm viel Raum für individuellen Stil. Ein Pokerspieler kann sich entscheiden, welche „hands” er spielen will, er kann Veränderungen wegen des Spielstils eines Gegners oder wegen der aktuellen Höhe der Einsätze vornehmen. Er kann ein Spiel durch einen Bluff gewinnen, ohne seine Karten aufdecken zu müssen. Manche „hands” haben von Anfang an einen gewissen Wert, andere sind zunächst wertlos, können aber später hohe Gewinne bringen, falls die richtige Karte gezogen wird.

Man kann Poker als genaue Annäherung an die Finanzmärkte sehen, und das Spiel ist ein nützliches Werkzeug, wenn man diese Konzepte besser verstehen will. Ich habe lange Zeit Analogien und Beispiele aus diesem Spiel herangezogen, um meinen Klienten zu helfen, die Konzepte des Vorteils zu verstehen, wenn wir daran arbeiteten, die Profitabilität ihrer Tradingstile zu optimieren. Da eine Pokerpartie stark durch die Persönlichkeit oder die Psyche ihrer Teilnehmer geprägt wird, ist dieser Analyseprozess wesentlich komplexer als ein einfaches Roulettebeispiel. Wegen des zusätzlichen „menschlichen Faktors” kann es erstaunliche Unterschiede zwischen dem mathematisch berechneten Vorteil und der Erfahrung in der realen Welt geben! Eine mathematisch perfekte Strategie nimmt an, dass die Gegner immer auf vorhersagbare Weise spielen, aber wie jeder Pokerspieler weiß, kommt das nur sehr selten vor. Der Einfachheit halber wollen wir annehmen, dass jede der nun beschriebenen Situationen an einem Tisch mit sechs Spielern vorkommt, an dem im Keller eines Freundes Texas Hold-em-Poker ohne Begrenzung der Einsätze gespielt wird. Beim Online-Poker oder beim Spiel in einem großen Casino zieht das „Haus” oder der Veranstalter direkt Gebühren ab. Diese Auswirkungen dürfen wir ignorieren, wenn wir annehmen, dass die Partie im privaten Rahmen stattfindet.

Wegen seiner Popularität im Fernsehen ist Texas Hold-em-Poker die beliebteste Pokervariante in modernen Casinos geworden. Jeder Spieler erhält zwei verdeckte Karten, und dann, nach einigen Bieterrunden, in denen die Spieler ihre Einsätze platzieren können, werden fünf Gemeinschaftskarten offen auf den Tisch gelegt. Jeder Spieler stellt sich aus diesen Karten die beste „hand” zusammen, und wenn es zum Showdown kommt, gewinnt die beste „hand” den „pot”, also die Summe aller Einsätze. Wenn die verdeckten Karten ausgeteilt worden sind, kommt es zu einigen Bieterrunden. Dann werden die ersten drei Gemeinschaftskarten (der „flop”) offen in die Mitte des Tisches gelegt. An diesem Punkt wissen die meisten Spieler schon, ob sie gute Karten haben oder nicht, und die meisten passen während der Bieterrunde, bevor die nächste offene Karte (der „turn”) auf den Tisch gelegt wird. Es folgt eine weitere Bieterrunde, dann wird die letzte offene Karte (der „river”) auf den Tisch gelegt. Nun gibt es keinen Raum mehr für Verbesserungen, und es folgt die letzte Bieterrunde.

Beginnen wir mit dem theoretischen Vorteil einer mathematisch perfekten Poker-Strategie. Wenn die ersten beiden Karten je zwei Asse, Könige, Damen oder Buben waren, beträgt die Wahrscheinlichkeit, gegen einen Gegner zu gewinnen 81 Prozent. Bei zwei Gegnern sind es nur noch 67 Prozent, also muss unsere Strategie Taktiken enthalten, die uns eine vorteilhafte Situation verschaffen. Unsere mathematisch perfekte Strategie besteht darin, nur diese vier „hands” zu spielen und dabei all unser Geld zu setzen, um alle Konkurrenten bis auf einen zum Ausstieg zu bewegen. Wie wir aus den vorherigen Beispielen wissen, besteht der erste Schritt bei der Analyse des Vorteils darin, die Wahrscheinlichkeit des Erfolgs zu definieren. Da wir nur mit zwei Assen, Königen, Damen oder Buben spielen wollen, gibt es nur 16 Karten, die für uns von Interesse sind. Die Wahrscheinlichkeit, dass die erste Karte ein Ass, ein König, eine Dame oder ein Bube ist, beträgt 16/52 oder 30 Prozent. Wenn wir das Glück haben, eine dieser Karten zu bekommen, haben wir eine Chance von 3/51 oder fast 6 Prozent, die richtige Karte für ein Paar zu bekommen. Anders ausgedrückt, beträgt die Wahrscheinlichkeit, dass wir sofort zwei Karten bekommen, die zu dieser Strategie passen, nur 1,8 Prozent (30 Prozent x 6 Prozent).

Wenn im Schnitt pro Stunde 50 „hands” verteilt werden, dann dürfen Sie erwarten, im Lauf eines dreistündigen Pokerabends zwei bis drei spielbare Kartenkombinationen zu erhalten. Wenn die Zwangseinsätze („blinds”) vor der Verteilung der Karten bei 50 Cent bis zu einem Dollar liegen, dürfen Sie damit rechnen, dass Sie im Lauf des Abends allein dadurch 37,50 Dollar verlieren. (Diese „Fixkosten” kann man mit den Transaktionskosten beim Trading an den Finanzmärkten vergleichen.) Wenn Sie mit 100 Dollar angefangen haben, dann ist es eine logische Annahme, dass sie davon noch etwa 80 bis 90 Dollar haben werden, wenn Sie die erste spielbare „hand” erhalten. Wir haben nun alle Parameter, die wir brauchen, um diese Strategie zu simulieren und Ihren rein mathematischen Vorteil zu definieren.

Wenn Sie einmal pro Woche drei Stunden lang Poker spielen, dann dürfen Sie damit rechnen, im Lauf eines Jahres 141 spielbare „hands” zu erhalten. Davon werden sie 114 gewinnen und 27 verlieren. Wenn jeder gewonnene oder verlorene „pot” im Schnitt 90 Dollar beträgt, sieht Ihr Gewinn im Gesamtjahr wie folgt aus:

114 Gewinne x 90 Dollar = 10 260 Dollar
27 Verluste x 90 Dollar = 2430 Dollar
Bruttogewinn 7830 Dollar – 1950 Dollar „blinds” = 5880 Dollar Nettogewinn

Bei 5880 Dollar dividiert durch 141 „hands” beträgt Ihre Gewinnerwartung knapp 42 Dollar pro „hand”. Natürlich gibt es Phasen mit Gewinn- oder Verlustserien, aber am Ende des Jahres wird die Zahl der „hands” hoch genug sein, um das auszugleichen. Wird sie das wirklich? Obwohl diese Pokerstrategie auf dem Papier hoch profitabel ist, würde ich garantieren, dass Sie in der realen Welt Geld verlieren, wenn Sie auf diese Weise spielen.

Die Realitätslücke

Da hier Menschen involviert sind, werden Urteile, Emotionen und Intuition Ihre Resultate stark verändern. Die Freunde, mit denen Sie ständig spielen, werden bald merken, dass Sie nur die vier obersten Paare spielen. Wenn sie sehen, dass Sie Ihren Einsatz erhöhen, werden sie passen, falls sie nicht selbst eine solche „hand” haben. Das bedeutet, dass Sie mit Ihren besten Karten nur selten einen großen „pot” gewinnen werden.

Schlimmer noch: Wenn ein Opponent dagegenhält, dann wird er das nur tun, weil er selbst extrem gute Karten hat. Diese Tendenz wird Ihren durchschnittlichen Gewinnprozentsatz drücken, und folglich dürfen Sie das ganze eben analysierte Strategiemodell vergessen. Ich nenne den Unterschied zwischen dem mathematischen und dem tatsächlich erfahrenen Vorteil die „Realitätslücke”.

Diese Realitätslücke ist der Grund, warum so viele systematische Tradingmodelle im Labor traumhaft aussehen, auf den realen Finanzmärkten aber nur zu Verlusten und Frustration führen. Zusätzlich zum mathematischen Potenzial einer Tradingstrategie muss man auch das Potenzial von Veränderungen am Markt analysieren. Wird sich diese Strategie auf den getradeten Markt auswirken? Wie wird sich die Performance der Strategie verändern, wenn das Marktumfeld ein anderes wird? Können Sie sagen, welches Marktumfeld den größten Vorteil bieten würde? Diese letzte Frage halte ich für die wichtigste.

Kaufen Sie dieses Buch über FinanzBuchVerlag

Leute lesen auch

• Jens Klatt – Trader - Der Weg zur profitablen Handelsstrategie - in jedem Markt
• Curtis Faith – Optimales Trading
• Magier der Märkte: Gemeinsamkeiten erfolgreicher Trader